Editor’s Note: The value interaction and collaborative learning is well documented. This article discusses practical steps for community building and poses some communication problems unique to mathematics and how they were solved.
Building Community in an
Online Upper-Division Mathematics Course
Markus Pomper
United States
Abstract
Learning can be a social experience, and creating a community of learners in a classroom can be an effective teaching tool. This case study suggests ways in which interaction between students in an online upper-division mathematics course can be used to create a virtual community of learners and help students master the concepts of proof in mathematics.
Keywords: real analysis, proof, class community, collaboration, online class.
Introduction
Online courses have become the medium of choice for students who cannot otherwise attend in a traditional classroom setting. Online distance education allows students to take courses in the convenience of their home or office, at their leisure, free of the distractions of campus life, without commute, while at the same time being provided with almost instantaneous access to instruction and an abundance of online resources. The critical reader may conjecture that the internet cannot replace a face-to-face meeting and that the dynamic of relationships between instructor and students (and among students) is not easily replicated in an internet class. Besides adapting course content for delivery in an electronic medium, the online instructor faces the additional task of fostering a sense of community among students who may never see each other face-to-face.
Cothrel and Williams (1999) define a “community” as a “group of people who are willing and able to help each other.” In the context of distance education, the necessity for building a community to facilitate learning is discussed extensively in the literature (e.g., Kirschner et al., 2004; Rourke, 2001; Northrup 2000; Weegerif, 1998, Gunawerdana, 1995; Cockburn, 1993). The consensus of this research is that the creation of a class community in online courses is desirable because it is a prerequisite for the social aspect of learning. Kreijns et al. (2004) argue that although social interaction in distance education courses is known to be important, “this aspect is often ignored, denied or forgotten by educators and researchers who tend to concentrate on cognitive processes and on-task contexts.” A successful distance education course harnesses the power of technology to create an appealing presentation of course material and utilizes tools of the internet to create an effective group dynamic so students can learn in a social environment.
Effectiveness of group learning in distributed learning groups depends on the social interaction that takes place. Kreijns et al. (2004) write that a “sound social space” has to exist so that learning in an online community can take place. They define a sound social space as one characterized by “effective working relationships, group cohesiveness, trust, respect, belonging, satisfaction, and a strong sense of community.”
The advantages of creating a social space and using it to enhance learning applies to all class settings, whether in a traditional classroom or in an online class. The task of creating this social space is conceivably more difficult in an online class, where physical remoteness and the lack of face-to-face interaction compound the fact that most students are not acquainted with one another. Kirschner et al. (2004) note that “if group members are initially not acquainted with each other and the group has zero history (which is often the case in distance education institutions), group forming, developing a group structure, and group dynamics are very important for developing a learning community. Otherwise, the risk is very high that learners become isolated and depressed because they are confronted with a lonely learning experience.” Likewise, Lock (2002) argues that a community is not a rigid entity. It is not in place on the first day of class, nor does it remain unchanged as the term progresses. Community, she argues, is a process, which is fluid in nature. An effective community of learners is nurtured and develops over time. Lock identifies four key aspects – communication, collaboration, interaction and participation – as the cornerstones that make the creation of an online learning community possible.
The purpose of this case study is to provide an account of how content-centered elements and asynchronous interaction between students were structured in an upper-division online mathematics course. The interaction among students allowed building of a sound social space in which students were able to discuss the content of the course. A system of discussion and peer review allowed students to develop the ability to read and write mathematical proofs. The next
section describes the context, content and the structure of the course. This is followed by a discussion of the course components that contributed to community-building and further the goals of the course. The last section describes some of the challenges faced in creating this course.
Context and Structure of the Course
The purpose of this article is to present a way of teaching a proof-heavy mathematics course (a first course in Real Analysis) in a distance education setting. The course explores the real number system from a rigorous perspective. Topics include Cardinality, Axioms of a Real Number System, Compactness, Sequences, Limits of Functions and Continuity. The course emphasizes formal proofs, both in presentation of the material and in students’ work. It is a required course for students majoring in Secondary Education in Mathematics and for students seeking a baccalaureate degree in Mathematics at Indiana University East. This regional campus of 2200 students located in East Central Indiana serves a rural area of seven counties.
Historically, Real Analysis has attracted only a handful of students, and more often than not was cancelled due to low enrollment. Offering this course in an online format produced the increased enrollment necessary to offer the course. During Spring 2007, 15 students enrolled – two students from as far away as Hong Kong. Almost all communication between instructor and students and among students was conducted through the internet. Indiana University’s course management system (Oncourse) was used to facilitate discussion using an electronic bulletin board. Course participants were technologically savvy and used the internet effectively for communicating. Most students used Microsoft Word Equation Editor for typing the mathematical symbols within their homework assignments. One student chose to submit scanned images of handwritten documents. Most course participants accessed the internet through a computer at home or at school, and most had a high-speed connection. One student reported using the computer at a public library because he found the dial-up connection at his home was too slow for loading course management system pages and sending large documents that contained his scanned pages.
Description of the Course Setup
The author is unaware of any recommendations or best practices specifically designed for web-based upper-division mathematics courses. In the more general context of web-based courses, Hill (1999) suggests (among other strategies) the need to create a “safe on-line environment”, an environment that the “learner perceives to be a space where open communication can occur without concern for flaming and non-constructive criticism.” Here, “flaming” refers to hostile and insulting criticism in the social context of the discussion board. This paper focuses on how this web-based course was structured so that a sound social space enabled productive collaboration in a community of learners.
The textbook for the course (Lay, 2005) was chosen because its writing style would enable students to follow most of the reasoning while reading independently. The author shows how a student should develop a proof – beginning with a rough draft, which would be refined until a complete proof was generated.
The material in the textbook was enhanced by instructor-created lectures on PowerPoint. In each PowerPoint presentation, the instructor attempted to recreate a lecture – with the obvious exception that students would not see the lecture develop live on a chalkboard. Each slide in the PowerPoint lecture would start with an empty screen and slowly be filled with text as the voice of the instructor explained what was happening. This mimicked the development of a topic on the blackboard in a physical classroom. The PowerPoint lectures followed the textbook closely and included additional verbal and written explanations.
Some pages contained animations that could not be reproduced in a print or chalkboard medium. The purpose of these animations was to provide students with mental models of the concepts under discussion. For example, a convergent sequence of real numbers could be represented by a “prototypical sequence” plotted in Cartesian coordinates, while an open set could be represented by the union of two open intervals (each represented as a line with hollow end-points). Fischbein (1982) and Thurston (1994) argue that these intuitive representations are a necessary precursor to formal mathematical thought. While the static images of convergent sequence and open set could be represented in print in a textbook (or on a blackboard in a traditional class), PowerPoint features were used to represent dynamic images. One example is an illustration of how an arbitrary open cover (represented by a large number of open sets) can be reduced to a finite subcover (represented by only three of the original open sets). The unneeded open sets migrate away from their original position and then fade into disappearance.
In creating the PowerPoint slides, the instructor continued the textbook author’s theme in developing a proof step-by-step, beginning with a review of the applicable definitions, and an analysis of how they would be used in order to prove the theorem at hand.
All discussion of the PowerPoint lectures and the homework problems was conducted on an internet message board. This board was part of a course management program,
One purpose of the online bulletin board was to create a sense of community in a group of students who may have never met in person. Some authors (Schwier & Balbar, 2002) suggest that a synchronous online discussion forum (for example a chat room) may be more successful in building a sense of community than an asynchronous forum (bulletin board). Schwier acknowledges that asynchronous discussion is superior for in-depth discussion of a topic. Therefore, the instructor chose an asynchronous forum as the only method of communication among the class. This mode of communication also permitted students to compose a comment containing mathematical symbolism in a way that others could read and understand. For example, a typical post might contain the following:
“I am currently trying to get started on Exercise 11.4. I was trying to follow the proof of theorem 11.7 in the text. However that leads me to a wierd [sic] contrapositive to prove. If x/=0, then x<0 or there exists e>0 such that x>e. (Note that e is epsilon).”
This student clearly understood what the statement asks her to prove. She used makeshift notation (/= instead of ≠, and e instead of e) and the readers may need some time to decipher this. She has put some effort into finding a valid way of proving the theorem and is asking her peers for advice as to how to continue. Posting this type of question in a synchronous conversation would most likely not be answered satisfactorily because students would have a hard time interpreting the makeshift notation, finding an answer, and then composing their answer in a suitable way. The message above was posted on a discussion forum at
As mentioned in the introduction, the purpose of the course is to acquaint students with the idea of a rigorous proof in the context of Real Analysis. Accordingly, most homework assignments asked students to contrive a proof of a stated theorem. Other assignments asked students to determine whether a given statement is true or false, and then either prove the statement (if true) or give a counterexample (if false).
When reading a textbook, students are typically presented with a polished version of a proof. This polished version – elegant, in the eyes of a mathematician – assumes that the reader is familiar with the basic proof techniques, that the reader has read the applicable definitions, and will not be surprised to see a proof start with the words “Let e > 0. Then choose d = min {1, ½ e2}.” While this phrase might spur the interest of a mathematician, an undergraduate student who is just learning how to prove theorems will undoubtedly be lost at the sight of these sentences. Where does the e come from and why should we choose d in this particular way? Students typically perceive this kind of proof as “coming out of nowhere” (Raman, 2003). What students don’t realize is that the proof went through several iterations before it took this form. In order to show students that the final version of a proof does not readily flow from an author’s quill, students were asked to discuss the proof first on the discussion board, then to submit a first draft of each proof, have it reviewed and critiqued by peers from the class, and then submit a final version.
The course syllabus outlined the expectations for the first and the final draft. In the first draft, students had to identify what would need to be done in order to prove the statement. They would also have to explain which definitions would be used in order to prove the theorem at hand. In the case of an e-d-limit statement, students would have to identify which quantity has to be less than e and how a series of estimates can be made to obtain a suitable value for d. The final version asked for a polished version of the proof – one that could be found in a textbook, which may be one that begins with the phrase “Let e > 0.”
The first draft would be submitted to the instructor, who would forward it to another student for review. For this purpose, there was a fixed due date for every homework assignment. When reviewing a peer’s paper, students were asked to evaluate the validity of the argument, suggest corrections if needed, and provide guidance for how the proof could be improved. The expectation for this exercise was that students would learn to appreciate the elegance of a finished proof, and understand that such a proof requires a series of drafts. The reviewing student would have a chance to see another student’s attempt at proving a statement, and would learn that there is usually more than one way of framing a valid argument. The instructor would critique all students’ proof suggestions and provide additional input for how a correct (or better) proof could be written.
The peer’s and the instructor’s critique were returned to each student, who would then revise the original draft; it would either become a correct proof, or a more elegant proof.
Besides the homework assignments, critiques and participation in the online discussion, there were no further written assignments. In order to discourage plagiarism, students were expected to be available for at least one telephone discussion with the instructor at some time during the semester. In this discussion, students were asked to explain their reasoning on a homework assignment. Most students were interviewed twice. Some students enjoyed this personal communication with the instructor and asked for additional interviews.
Examples of Some Course Work
The graphic reproduces some of the PowerPoint Slides from Section 13 of the textbook – “Topology of the Real Numbers”. This section was covered at approximately mid-semester. By this time, students were proficient at viewing the PowerPoint lecture. The pictures below are examples of several slides from the lecture. Each slide begins with an empty page. A narration explains what is being done, and the text appears one line at a time. The two slides titled “Example 13.15” are examples of a graphic to which details are added as the explanation progresses. This is to allow students to build a mental model of the Natural Numbers as a subset of the Real Numbers, and of the concept of “not being an accumulation point”.

Figure 1. Examples of PowerPoint Slides
The stop signs invite students to perform a task and break the monotony of the PowerPoint lecture. The entire lecture for Section 13 contains 54 slides and takes approximately 60 minutes to play if no breaks are taken. It can be conjectured that students might spend twice this length of time if they replay some portion of the presentation or if they take notes as they watch the presentation. The entire section represents one week’s work. The last slide invites the students to try Exercise 13.15 on their own. In fact, this problem was assigned as a homework problem.
Problem 13.15. Prove: If x is an accumulation point of the set S, then every neighborhood of x contains infinitely many points from S.
The proof of this statement is not a purely syntactic one, that is, it cannot be achieved merely by an instantiation of a Definition or a previously proved Theorem. It requires some insight topology of the Real Numbers. Weber (2002) argues that undergraduate students often lack the strategic direction for writing a valid proof. In order to help students overcome this hurdle, each problem usually included a hint as to how it could be started. The instructor provided the following guidance on the problem: “Analyze the statement, and then consider a contrapositive or a contradiction”.
Students discussed the problem in the online discussion forum in the manner below. (The names of the students have been changed to protect their identities.) Note that the discussion threads span a time of 48 hours, and that most questions are answered within 36 hours of the start of the thread. In this discussion, there was no input from the instructor, however most discussion threads did require some intervention.
In this thread students treat each other cordially and appear to have an interest in answering each others’ questions; this is typical for all discussions that took place in the course.
Author: Adam |
Author: Bryan | ||
Author: Cheryl | ||
Author: Bryan |
Author: Adam |
Author: Donna |
Author: Cheryl |
Below is Donna’s first draft of the proof. She followed the instructions for this assignment
Exercise 13.15 Prove: If x is an accumulation point of the set S, then every neighborhood of x contains infinitely many points of S. ¶ Analysis: The statement is of the form pÞq where p: x is an accumulation point of the set S q: every neighborhood of x contains infinitely many points of S. The contrapositive would be of the form ~qÞ~p. In this case, ~q: there exists a neighborhood of S which contains a finite number of elements of S. ~p: x is not an accumulation point of the set S Therefore in order to prove the original statement we can prove the contrapositive which says, “If there exists a neighborhood of S which contains a finite number of elements of S, then x is not an accumulation point of the set S.” In order to prove the contrapositive, we need to find a neighborhood of x that contains a finite number of element of the set S and show that for all e>0, N*(x;e)ÇS=Æ. That is, we will show that for a point x, there exists a deleted neighborhood of x that does not contain a point in S. Further suppose that x is an accumulation point of S. If x1 is the closest point in N(x;e) to the accumulation point, then e1=|x-x1| where e1 is the radius of the neighborhood by definition 13.1. Since x1 is the closest point of N(x;e) to x, all points in the smaller neighborhood N(x; e1) will be within the radius e1 from x. By definition 13.14, a point x in R is an accumulation point of S if every deleted neighborhood of x contains a point of S. In this case, N*(x; e1) does not contain any points of S, and therefore we conclude that N*(x;e)ÇS=Æ. Because N*(x;e)ÇS=Æ, x is not an accumulation point of the set S as required. This proves the contrapositive of the original statement and we conclude that “If x is an accumulation point of the set S, then every neighborhood of x contains infinitely many points of S”.¨ |
This first draft was followed by a peer critique. The student commented on Donna’s paper:
Critique: You say “Suppose S⊆R and there exists a neighborhood N(x;ε)={x1, x2, x3, …,xn} which contains a finite number of elements of S.” This is ~q. And then you say “Further suppose that x is an accumulation point of S.” This is p. In your setup, I think that you are doing (−q∧p) →c, or prove by contradiction by not prove by contrapositive. |
Exercise 13.15 (5 pts) Make your final draft more concise. Omit the analysis. Begin your proof with the statement “We argue by contradiction: Assume that x is an accumulation point and that there exists a neighborhood N(x, e) about x that only contains finitely many points.” Correct the statement N(x, e ) = { x1, x2, … xn }. This would mean that the neighborhood itself only contains finitely many points. What you mean is that the neighborhood contains only finitely many points from S (other than, possibly, x itself), which would be N*(x, e ) Ç S = { x1, x2, … xn }. The same correction must be done further down in the proof. |
Donna followed up on the recommendations and provided the following proof in her final draft. Note that the proof is more polished than the first draft, but still is not perfect. It is clear that the student incorporated ideas from both her peer and from the instructor. This student also reviewed one of her peers’ papers, so it is possible that she used some of the ideas of that paper in guiding her revisions.
We will argue by contradiction: Suppose x is an accumulation point and that there exists a neighborhood N(x;e) about x which contains only finitely many points of S. That is N* (x;e)ÇS = {x1, x2, x3, …,xn} If x1 is the closest point in N(x;e) ÇS to the point x, then e1=|x-x1| where e1 is the radius of the neighborhood by definition 13.1. Since x1 is the closest point of N(x;e) ÇS to x, all points in the smaller neighborhood N(x; e1) will be within the radius e1 from x. By definition 13.14, a point x in R is an accumulation point of S if every deleted neighborhood of x contains a point of S. In this case, N*(x; e1) does not contain any points of S, and therefore we conclude that N*(x;e)ÇS=Æ. Because N*(x;e)ÇS=Æ, x is not an accumulation point of the set S as required and we conclude that “If x is an accumulation point of the set S, then every neighborhood of x contains infinitely many points of S”.¨ |
Discussion and Conclusion
In discussing the value of online learning, Kirschner et al. (2004) cite the formula
Valued Learning Experience = F (pedagogy, content, community),
where the function F has the property that if any of the three independent variables approaches zero, so does the value of dependent variable. The discussion will center on the pedagogy and the community aspects of this formula.
Pedagogy - Textbook and PowerPoint Lectures
The textbook and the PowerPoint lectures provided students with the mathematical content for the course. These two elements alone would have made the course into a glorified independent study – a course where there is no interaction among students, and only limited interaction between student and instructor.
From conversations with students, it appears that most used the textbook and the PowerPoint lecture while studying the material. Some students reported annotating the textbook, while others kept a journal with their notes. One student posted the following message on the discussion board during the first week of classes:
“If anyone has not yet looked at the PowerPoint slides, I highly recommend you doing so. Everything is pointed out very clearly with good examples. They are easy to read and listen.”
The comment was followed up by several others, agreeing to the post. In private conversations, students praised the lectures because they could replay individual slides and because the animated diagrams provided them with a mental model that helped them understand the concepts.
The purpose of requiring students to participate in an online discussion forum was to create a sense of community in which learning can take place. With few exceptions, students posted comments and questions during each week of the semester. The most prolific writers posted more than 200 messages throughout the term. The two least prolific writers (of those students who finished the course) posted between 50 and 60 messages.
The instructor participated in the discussion as well, posting over 500 messages during the semester.
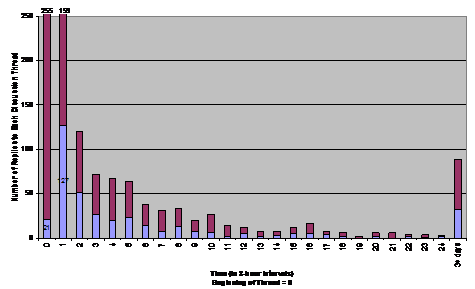
Figure 2. Elapsed Time to responses for each thread in a discussion forum
The graphic displays the elapsed time between the initial posting of a message in the discussion forum and all follow-up postings in response to this initial posting. (Students’ postings are in purple, and instructor’s postings in blue). The initial posting of a message occurs at time 0. The responses are grouped in intervals of 3 hours. Therefore, Time interval 1 means than an answer was posted within three hours of the initial message, 2 means that the answer was posted between 3 and 6 hours from the original message, etc.
Most of the discussion threads were student-initiated (255 threads versus 21 threads that were instructor initiated). The instructor replied to most initial threads within 12 hours of posting, but this initial interaction was usually intended to clarify the original question, to acknowledge that the question had been read, or to give a minor hint as to where the answer to the question could be found. Most of the discussion occurs within the first 24 hours of the initial posting of the message (the first eight 3-hour blocks). Discussion of the topic almost entirely ceases after the second day. A review of the discussion threads suggests that students were satisfied with the answers they received and hence saw no need to continue the thread. If a wrong attempt was posted in a discussion and students did not continue the discussion (believing that a correct answer had been found), the instructor would revive the thread by pointing out the mistake.
In conclusion, the use of the discussion forum proved an effective tool to involve students in collaborative efforts to understand the course material and to devise mathematical proofs.
A Community of Learners
The concept of a community is one of the central tenets of a valuable experience. The purpose of this section is to discuss whether the course format allowed a community to form. Schwier (2001) enumerates four characteristics of communities as being hospitable, having life cycles, being multifaceted and being resilient. Kreijns et al. (2004) argue that a sound social space is a requisite for the social aspect of learning in a community. The purpose of this section is to illustrate that the online discussion did indeed foster a community. Collaboration among students helped them develop an understanding of the concepts of Real Analysis.
Students who are freshly exposed to a new concept are usually not quite sure whether they fully understand the concept. The discussion forum was intended for students to test and discuss ideas in the context of the course content. It allowed them to overcome the feeling of uncertainty about a new concept, or clarify any misconceptions. Admitting that one feels uncertain about a new concept puts the student at risk of being ridiculed by his/her classmates. In his initial post (above), Adam asks two questions:
“Do you know how to write this statement in sentence? I don't know how to translate "infinitely many points of S" to mathematical symbols.”
He admits not knowing how to translate a verbal statement into a mathematical one, and potentially opens himself up to criticism. The fact that he nevertheless asks the question is an indication that he trusts that his peers will not ridicule him, “flame” him, or subject him to unconstructive criticism.
The discussion that followed Adam’s post is an indication that students did indeed develop a good working relationship in the class. In collaboration they analyzed the statement, found ways how to express a verbal statement into a mathematical one, and then discovered the key idea of the proof, namely that of a neighborhood of a given point x contains only finitely many points from S, then one of those points must have minimum distance to x.
The mathematical aptitudes of the students were quite varied, and some of the questions posed by the weaker students must have appeared trivial to the stronger ones. Nevertheless, there was never any critical or discouraging word posted in reply to a trivial question. In fact, the stronger students readily volunteered to answer (as well as they could) the weaker students’ questions.
Consider the following messages regarding a detail that arises in solving a particular problem. Within this problem, students would need to solve the equation
for y. The appendix provides students with this solution,
|
Frank clearly has trouble with basic algebra. Nevertheless,
Judging by the content of the discussion forum, students clearly took an interest in each others’ progress in the course. The discussion forum provided a safe place for conversation – students could (and indeed did) ask questions and participated in discussion without being “flamed” or subjected to other non-constructive criticism. As such, the discussion forum met the standards of one of Hill’s (1999) best practices for creating a community of online learners, and one of the characteristics of Kreijns’ et al. (2004) “sound social spaces”. The discussion in the course provided a hospitable environment where students could test their ideas.
An unexpected side effect of the online discussion was that some students began to communicate with one another outside of the discussion forum. This phenomenon has been observed before. Schwier and Balbar (2002) compare these out-of-sight conversations to students whispering to each other during class, or passing notes. The instructor became aware of the “whispering” because students referenced their study-buddy’s help when handing in the homework assignments. At least two such virtual study-buddy pairs formed, which is considerable, given the class size of 9 students after mid-semester. Those students also continued their participation in the discussion forum, so the rest of the class did not lose their input after the study-buddies formed.
Kreijns et al. (2004) argues that a sound social space enables effective collaboration. They define a social space as the network of social relationships between members. Thus, the development of study-buddy pairs who collaboratively work on course assignments indicates that the online discussion format was successful in creating a sound social space. In Schwier’s (2001) terms, this forming of study-buddy pairs reaffirms that communities tend to find ways organize and redefine themselves – they find ways to adapt to external constraints. In this class, some members of the group found that the discussion in the online forum did not suit their needs. They overcome this hurdle by mutating and finding a way to bypass this perceived obstacle: In this example, the students chose to communicate via email and telephone, in addition to the discussion forum.
Naturally, most of the discussion in the forum centered about course content. Some discussion threads, however, branched off and took on a different perspective. Consider the discussion between two students:
Author: Adam Any ideas? |
Author: Cheryl |
Author: Adam |
Author: Cheryl |
Author: Adam |
Here, students discuss the meaning of the word “hypothesis”. In doing so, they consider economics and statistics; they use a Wikipedia reference in clarifying the term “Hypothesis”. In a sense, the discussion about the meaning of the term “hypothesis” is irrelevant to content of the course. It did, however, appear important to the students and they took the time to discuss the term. This slight off-topic discussion is an indication that students feel that the discussion forum is a place to discuss topics that are important to them, and that they feel safe at doing so.
As the semester ended, students posted these comments on the discussion board:
Author: Bryan |
Author: Cheryl |
Author: Adam |
The discussion here illustrates that students – in some way – cared about each other.
It appears that these students valued each other’s presence in the online class; their messages are personal and might even express some sort of melancholy about the imminent end of the course. It may be conjectured that student interaction through peer review and online collaboration created cohesiveness among the group. Indeed, some of the students kept up their collaboration for some time after the official end of the course, which suggests that the collaboration did not only occur because it was a course requirement, but because students took an interest in working with their peers.
Synchronous or Asynchronous Discussion?
One might ask whether a synchronous discussion might have been more advantageous in creating such an online community. The technological limitations of the course management software used here would not have allowed for writing mathematical symbols in “real-time”. Even though this technical difficulty might be overcome in the future, a more philosophical issue is whether finding a quick response to a hastily posed question (as would be the case in a chat room) is desirable in mathematics. After all, mathematicians pride themselves in finding concise ways of asking a question and in polishing their proofs. This, of course, takes time, and an online discussion forum might be the preferable way of teaching students a mathematician’s way of thinking.
A more practical perspective arises from the convenience an online course offers students. They are not bound by a particular class schedule and may complete the assignments when their schedule permits. The table below shows the number of postings to the discussion board as a function of the time of the day. With the exception of the early morning hours, there is no specific time of day during which students prefer to participate in class. Setting a specific time at which the entire class would participate in an online chat would therefore take away some of the freedom students gained by taking the online class.
Given that the asynchronous discussion forum was able to generate a community of learners, the practical and philosophical disadvantages appear to outweigh the benefits (Schwier & Balbar, 2002) of synchronous discussion.
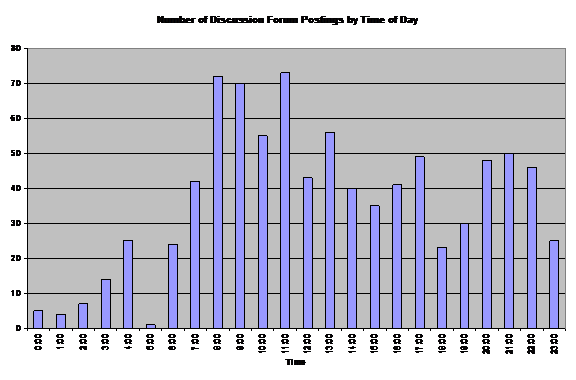
Figure 3. Time of access
Challenges
One of the challenges in this course was that not all students participated equally well in the discussion forum. As explained earlier, there were two students who only contributed between 50 and 60 times to the discussion forum during the semester, while all other students contributed more than 150 times. This lack of participation is not due to the fact that students had no access to the internet: One of those students accessed the course website more frequently than some of the most prolific writers. The other student spent more time logged into the course website than most other students. A review of the content of the messages these two writers posted does suggest that they did not grasp the material well enough to even formulate a valid question. (Frank’s posting above is one of them). That is, those students did not participate in discussions because they likely had nothing significant to contribute. In fact many of these students’ postings contain trivialities like “I understand now,” despite the fact that their homework assignment suggests otherwise.
Lack of preparation and inability to understand content are of course challenges in every class, online or not. As in a traditional format, those difficulties manifest themselves in lack of participation and poor performance on assignments.
Another challenge in this course was a high non-completion rate. Of an initial enrollment of 15 students, only 8 completed the course with a passing grade. The remaining seven withdrew officially (5), were administratively withdrawn for financial reasons (1), or gave up without officially withdrawing (1). Those students who withdrew typically stated or implied that they were underprepared and could not find the time to make up for this lack of preparation. Even those students who remained enrolled contended that the time required to succeed in this course was more than they had anticipated. The investment of time for interacting in an online environment can be 2-3 times higher than in a face-to-face course (Palloff & Pratt, 1999), and in this regard the course at hand was not an exception. The course setup may therefore be well in line with other distance education courses. Nevertheless, a high non-completion rate is unsatisfying to the instructor. Providing more guidelines for time-management could help students in this situation. The learning community was effective in supporting the work of academically prepared students. Their work suggests that discussion and collaboration helped them achieve the goals of the course. The community was not able to remediate the deficiencies of the academically underprepared students. Those students contributed little to the group’s efforts at solving problems. It may be argued that the community marginalized those two students, or that those two distanced themselves from the community.
Conclusion
In summary, it appears as if the course structure was successful in creating a community of learners – a group of persons who are willing and able to assist each other in their learning. The structure was equally successful at creating a safe learning environment, where students could contribute to the discussion without fear of non-constructive criticism. The group dynamic was used successfully in helping students understand Real Analysis and gain an initial understanding of how to write a formal proof. Of course, this study only relies on one instantiation of this course, and can therefore not easily be generalized. Nevertheless, it is clear that community can be created in an on-line upper-division math course, while maintaining the academic standards of the course.
References
Cockburn, A., & Greenberg, S. (1993). Making contact: getting the group communicating with groupware 1993. In: Proceedings of the Conference on Organizational Computing Systems (COOCS ’93). Milpitas, CA: ACM Press, 31–41.
Cothrel, J. & Williams, R. L. (1999) Online communities: Helping them form and grow. Journal of Knowledge Management, (3)1, 65-60.
Fischbein, E. (1982) Intuition and Proof. For the Learning of Mathematics. 3(2), 9-24.
Gunawardena, C.N. (1995). Social presence theory and implications for interaction and collaborative learning in computer conferences. International Journal of Educational Telecommunications 1, 147–166.
Hill, J. (1999) Building Community in Web-based Learning Environments: Strategies and Techniques. Available online http://ausweb.scu.edu.au/ aw01/ papers/ refereed/ hill/ paper.html
Kirschner, P.A. & Van Bruggen, J. (2004) Learning and Understanding in Virtual Teams. CyberPsychology & Behavior, 7(2),
Kreijns, K.; Kirschner, P.A.; Jochems, W. & Van Buuren, H. (2004) Determining Sociability, Social Space, and Social Presence in (A)synchronous Collaborative Groups. CyberPsychology & Behavior, 7 (2): 155-172.
Lay, S. (2005). Analysis with an Introduction to Proof. Upper Saddle River, NJ: Prentice Hall.
Lock, J.V. (2002). Laying the groundwork for the development of learning communities within online courses. The Quarterly Review of Distance Education, 3(4): 395-408.
Northrup, P.T., & Rasmussen, K.L. (2000). Designing a web-based program: theory to design 2000. Presented at the Annual Conference of the Association for Educational Communications and Technology, Long Beach, CA.
Palloff, R. M., & Pratt, K. (1999). Building learning communities in cyberspace: Effective strategies for the online classroom. San Francisco, CA: Jossey-Bass.
Raman, M. (2003). Key Ideas: What are they and how can they help us understand how people view proof? Educational Studies in Mathematics, 52: 319–325.
Rourke, L. (2001). Operationalizing Social Interaction in Computer Conferencing. Available online http://www.ulaval.ca/aced2000cade/francais/Actes/Rourke-Liam.html
Schwier, R.A. (2001). Catalysts, Emphases, and Elements of Virtual Learning Communities – Information for Research and Practice. Quarterly Review of Distance Education, 2(1): 5-18.
Schwier, R.A., & Balbar, S. (2002). The Interplay of Content and Community in Synchronous and Asynchronous Communication: Virtual Communication in a Graduate Seminar. Canadian Journal of Learning and Technology, 28(2).
Thurston, W. P. (1994). On proof and progress in mathematics. Bulletin of the American Mathematical Society. 30, 161-177.
Weber, K (2002). Student difficulty in constructing proofs: The need for strategic knowledge. Educational Studies in Mathematics 48: 101-119.
Wegerif, R. (1998). The social dimension of asynchronous learning networks. Journal of Asynchronous Learning Networks 2:34–49.
About the Author
Markus Pomper
is Associate Professor of Mathematics at Indiana University East,email: mpomper@indiana.edu