Editor’s Note:  Educators talk about thinking “outside of the box”. This paper uses three dimensional graphics to facilitate problem solving, creativity, and higher levels of learning.  Dr. Abumosa explores math ideas and new approaches to math education using a Geometers SketchPad ( GSP) and Dynamic Geometry Software .

Using a Dynamic Software as a Tool
for Developing Geometrical Thinking

Mofeed A. Abumosa

Jordan

Abstract

This paper researches the relationship between van Hiele theory and its levels of geometric thinking with the dynamic software program geometry sketchpad. The paper reveals the harmony between the Graphic SketchPad (GSP) software and the van Hiele theory. Moreover, it suggests a method of using GSP to teach geometry in schools and using it as a tool to develop geometric thinking. Examples show and explain how GSP was used to develop a new theory from Pythagorean Theorem.

Keywords: geometric thinking, van Hiele theory, dynamic software, graphic sketchpad, GSP, technology.

Introduction

Principles and Standards for School Mathematics document (NCTM, 2000, p42) identifies the foundations of quality mathematics that should be taught in schools. It clears that "through the study of geometry, students will learn about geometric shapes and structures and how to analyze their characteristics and relationships and geometry is a natural place for the development of students' reasoning and justification skills, culminating in work with proof in the secondary grades".

Principles and Standards for School Mathematics document also clears the role of Technology in the teaching and learning of geometry. Tools such as dynamic geometry software enable students to model, and have an interactive experience with, a large variety of two-dimensional shapes. By using technology, students can generate many examples as a way of forming and exploring conjectures, but it is important for them to recognize that generating many examples of a particular phenomenon does not constitute a proof. Visualization and spatial reasoning are also improved by interaction with computer animations and in other technological settings (Clements et al. 1997; Yates 1988).

The attempt to develop a comprehensive theory that describes how students learn specific mathematical domains or concepts is rather rare in the field of mathematics education. A prominent example is the Van Hiele theory; the most comprehensive theory yet formulated concerning geometry learning. It was developed by Pierre and Dina van Hiele almost half a century ago (Evan, Ruhama & Tirosh, Dina, 2003). The theory claims that when students learn geometry they progress from one discrete level of geometrical thinking to another. This progress is discontinuous and the levels are sequential and hierarchical. The Van Hiele theory also suggests phases of instruction that help students progress through the levels.

Problem/Research Questions

The rapid development of computer technology adds new pressure on math educators. The ease of using computer software and the drop in their prices put math educators in front of a big question: How computer technology can be used to enhance math learning and teaching?. The "How" question was the motivate factor behind this paper.

Specifically, this paper tries to answer these questions:

1. How dynamic software like GSP can be used as a tool of developing geometric thinking?
2. How dynamic software like GSP can be related to Van Hiele theory?

The attempt of answering the questions is based on analyzing the characteristics of GSP and look for its' harmony with Van Hiele theory.

Theoretical framework

Hoffer invented a two dimensional matrix to represent geometrical thinking: the first dimension consists of five geometrical skills (Visual, Descriptive, Drawing, Logical and Applied). The second one deals with the levels of geometric thinking (Recognition, Observation, Analysis, Ordering, Deduction and Abstraction). (Hoffer, 1981, p15). This paper restricted with three geometric skills (Visual, Descriptive and Logical) and three levels of geometrical thinking (Recognition, Analysis and Deduction).

Table 1

Levels of geometric thinking distributed according to levels of geometric skills

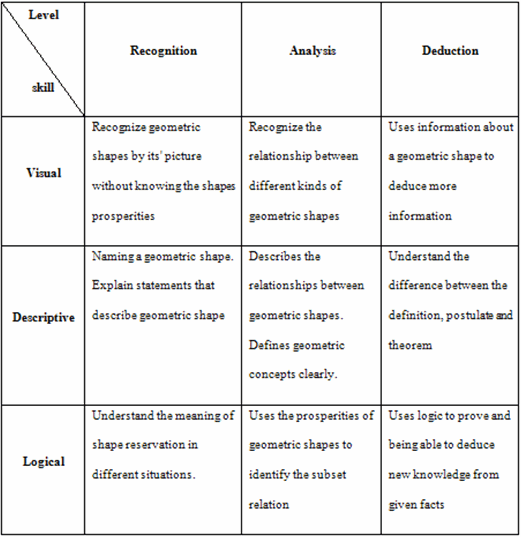
The previous matrix is considered as a tool for proving the harmony between GSP and van Hiele theory. The previous matrix can be translated into a pyramid of three levels. Figure (1) demonstrates the three levels.

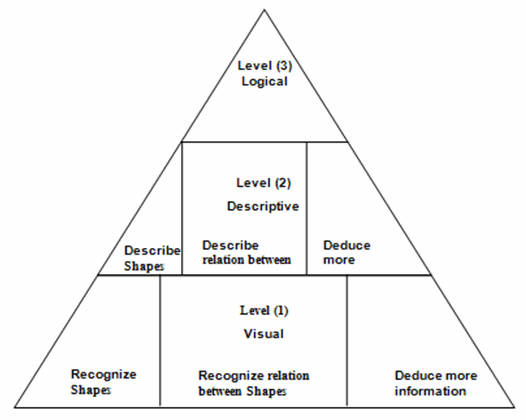
Figure 1. Pyramid of three levels of geometric thinking

Procedure

The procedure of this paper based on analyzing the characteristics of GSP and look for its' harmony with Van Hiele theory which answers the second question. The procedure of answering the first question is based  on the idea of show me how. So an example of discovering a new theory will be introduced showing the process and the reflections the researcher has done. 

According to the Geometer's Sketchpad Workshop Guide (Chanan,2002), and the personal experience of the researcher with GSP, the trainee starts with recognizing basic concepts ( Point, Compass, Straightedge) to use them in constructing shapes (circle, square…): I considered that as level one (Visual). When you move to the next section of training you will learn to explain and describe shapes visually, which happens through drawing a shape the way he likes. In practicing the construction with GSP you will learn to recognize the relationship between different shapes and in every activity the trainee is challenged to do the same activity in another way or deduce more information. The reader can see the match between the levels of thinking and the GSP by practicing the work.

Example

Tour (1) in the GSP training guide is: constructing a square. The way it is explained matches the levels of thinking mentioned in Fig (1). A trainee can construct a square in many ways:

1. Draw segments (parallel and perpendicular) and try to make them congruent by daggering the points (level (1)).
2. Construct a grid and join between points on the grid level (1) see Fig (2).
3. Construct a circle and perpendicular and parallel lines level (2) see Fig (3).   
4. Using transformations to do the construction level (2).
5. Use the measure tool to justify your work level (3)
6. Do the same construction in other ways level (3)
7. Ask the trainee to prove the construction in an abstract way level (3).

When you move on with the training guide you will easily see the harmony between GSP and van Hiele theory. While working actively with the software users can and should master geometric concepts, theorems, skills and problems. GSP is considered as a comprehensive thinking tool. So, I recommend the curriculum writers to adopt GSP not only as an auxiliary tool but to build the activities in a way that makes the advantage of the software is max.

It can be seen easily that most of geometric constructions can be done the same way. So, I suggest that curriculum experts can rebuild all the geometry content in a way to make advantage of such dynamic software.

How GSP can also be used for teaching geometry?

By using GSP students can construct geometric shapes, describe the relation between them, discover and prove new theorems. By using the Custom Tool teachers can follow the thinking of every student and assess the level he (she) reaches, since the Custom Tool shows the steps the student follow to accomplish the assignment. 

Figure (4) shows the script of drawing a square by using the circle and the script of drawing the same shape by using the transformation tool. It is clear that such tools as so important in developing metacognition skills. 

I was impressed by the previous theoretical frame and start to investigate how the dynamic software can be used as a tool of thinking in geometry.

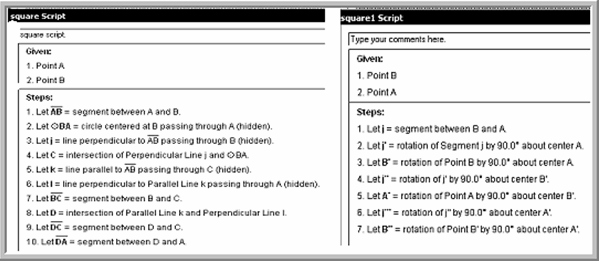
Figure 4. The script of drawing a square

A New Theory:

I start reading many studies that dial with dynamic software and geometry for example Hollebrands (Hollebrands, 2007), investigated the ways in which the technological tool, "Geometry Sketchpad", mediated the understandings that high school Honors Geometry students developed about geometric transformations by focusing on their uses of technological affordances and the ways in which they interpreted technological results in terms of figure and drawing. The researcher identified purposes for which students used dragging and different purposes for which students used measures. These purposes appeared to be influenced by students' mathematical understandings that were reflected in how they reasoned about physical representations, the types of abstractions they made and the reactive or proactive strategies employed.

But I was attached by Ron's Theorem (MeAlister & others 2004). Ron MeAlister, a middle school teacher, becomes fascinated with geometric patterns produced with GSP, explored an idea, conjectured a result, and proved it (Jackiw, 1995).

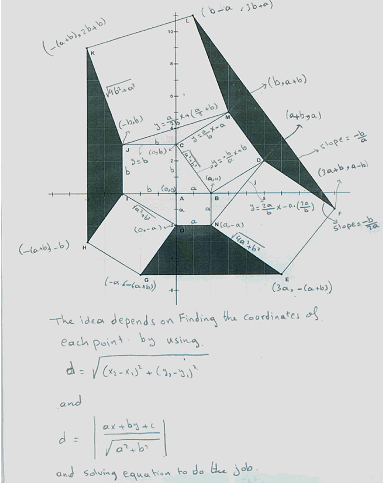
Ron was a trainee in one of the professional development workshops. It was about using GSP in finding geometric patterns, exploring, and conjecturing. During the workshop, Ron came upon a nice result while using GSP to explore the Pythagorean Theorem. His theorem is illustrated in the figure (5).

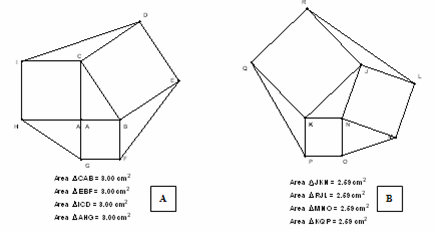
Figure 5. Ron’s Theorem and its extension

The theorem says that when you construct squares on the sides of any triangle and join the ends to form new triangles then the area of the new triangles and the original one are equal.

In fig (5) A, the area of the right triangle ABC is 3 cm2 which is the same as the area of the other three triangles shaded in yellow. Fig (5) B shows the same result with a triangle which not right.

Ron constructs a mathematical proof that depends on sine law and cosine law. Ron's work illustrates the way GSP should be used "can make and extend conjectures easily" (NCTM, 2000, P25). Ron's severed as a springboard for other geometrical discoveries. He said "this discovery has inspired me to understand and enjoy geometry more than I ever thought I would" P150.

While I was working as a subject matter expert in preparing e-math curriculum in Jordan, Ron's discovery inspired me, and opens my mind to prepare the e-math content toward thinking and problem solving. So, I start working on GSP to discover geometry content in my way employing my knowledge with mathematics and teaching. My way to do things depends on recreation of what we know that I think leads to new knowledge, and new methods of teaching both the students in schools and teachers in education programs.

My new theory

Depending on Ron's theorem I construct new squares on the sides of triangles Ron has built. And join the end points to have trapezoids see fig (6) starting with right angled triangle. The theorem states that the areas of the trapezoids are equal, and if we continuo the construction in the same way it can be seen that the areas of trapezoids in each step are equal. Then I tried to change the core triangle to be not right see Fig (7) I still have the same result. 

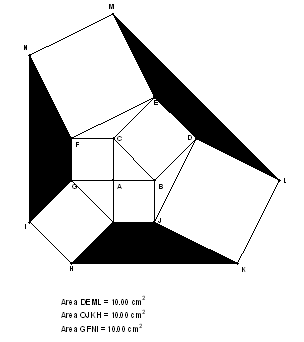
Figure 6. The new Theorem (the core triangle is right)

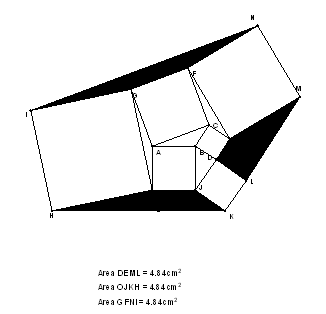
Figure 7. The theorem with a core triangle not right

Other Figures showing the same theorem

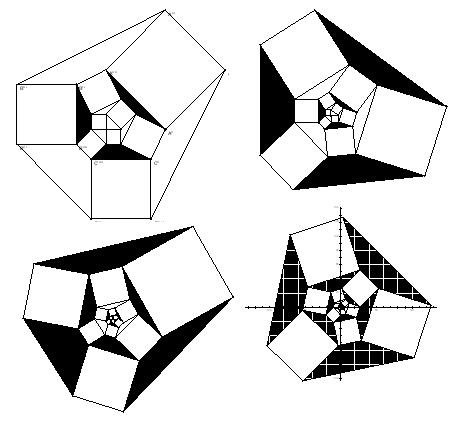
Figure 8. Figures showing the same theorem

The previous shapes shows the theorem when the pattern continuous.

The following figure illustrates an idea of proving the theorem.

Figure 9. The idea of the proof

At last I tried to discover a relation between the area of the origin triangle and the area of constructed trapezoids

Table 2

Discovering relationship between area of core triangle and areas of trapezoids

The previous table shows the areas of the origin triangle in different situations and how it relates to the areas of trapezoids. I don’t have the time to finish the work so I do it by excel and fin the best fit polynomial that represents the relation.

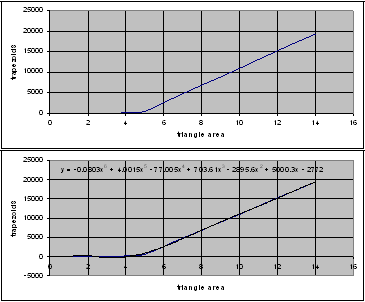
Figure 10. Using Excel to find the best fit function

It can be seen easily that the geometric pattern can be converted into algebraic one.

Conclusion

The paper suggests a method of using dynamic software (GSP) as a tool of developing geometric thinking which can be summarized by the following steps:

1. Find an old theory in geometry.
2. Use GSP to revisit the theory.
3. Ask your self " WHAT IF" and start using GSP to discover.
4. Justify your thinking.
5. Prove your conclusion.

  Most of old theorems can lead our students to new ones.

 References

1.  Chanan, Steven & others (2002). Geometer's Sketchpad Workshop Guide. Key Curriculum press 2002.

2.  Evan, Ruhama & Tirosh, Dina, 2003. Teacher Knowledge and Understanding of students' Mathematical Learning. Hand Book of International Research in Mathematics Education. Lawrence Erlbaum Association 2002.

3. Hoffer, A. (1981). Geometry is more than proof, Mathematics Teacher, 74, 11-18.

4.  Hollebrands, Karen F, 2007. The Role of a Dynamic Software Program for Geometry in the Strategies High School Mathematics Students Employ.  Journal of Research in Mathematics Education. Vol 38, No. 2, 164-192.

5. Jackiw, Nicholas, The Geometry's Sketchpad. Emeryville, Calif: Key Curriculum Press, 1995.

6. MeAlister Ron, Martinez-Cruz Armando and Gannon Gerald (2004). Ron's Theorem and Beyond: a True Mathematician and GSP in Action. Mathematics Teacher. Vol. 97, No. 2. Feb 2004. PP 148- 151.

7. خصاونة، أمل (1994). مستويات التفكير في الهندسة لدى الطلبة المعلمين، أبحاث
اليرموك، المجلد العاشر، العدد الأول، ص ص

 439 – 481.

About the Author

Mofeed A. Abumosa, PhD Curriculum & Instruction- Math Education
Faculty of Education, Arab Open University- Jordan Branch,
Jordan, Amman, P.O Box 240872, code 11121

M_abumusa@aou.edu.jo

mofeedabumosa@yahoo.com

Technical Note:

GSP stands for The Geometer's Sketchpad®. It was used in conjunction with Dynamic Geometry® Software for Exploring Mathematics, Version 4. Visit http://www.keypress.com/x5521.xml  for information about the software

According to Dr. Abumosa: “I purchased the software last year and started training on it . Readings in Mathematics Teacher (NCTM) led me to use the software to explore new math ideas for both math and math education. This software is dynamic. It enables the user to measure length, area, etc…, it enables construction of geometric objects based on the idea of the father and child, so it gives the mathematician, the math teacher and students an opportunity to discover new concepts in mathematics and employ new techniques in teaching geometry.”