Editor’s Note: With the move toward Universal Health Care in the United States, there is a growing interest in the economic impact of various reimbursement policies. The economic impact of various decision models is studied next..

Teaching Healthcare Reimbursement Systems Using System Dynamics Models

Michael H. Kennedy

USA

Abstract

Methods for reimbursing healthcare providers and facilities are frequently taught in courses addressing healthcare finance.  Unfortunately, defining the method of reimbursement and illustrating solutions to various problems incorporating these reimbursement methodologies often fail to convey the dynamic nature of payment systems or to set the context for informed decision-making.  System dynamics software provides an appropriate medium for demonstrating the flow of funds associated with healthcare reimbursement and for illustrating the impact of typical management decisions.  Three reimbursement methods are modeled generically: cost-based reimbursement, prospective payment, and capitation.

Keywords: Finance, health care, payment systems, system dynamics

Introduction

Financing healthcare in the United States is not a static enterprise.  Getzen (2007) uses a “flow of funds” approach to characterize the dynamic nature of financial transactions.  Premiums and tax dollars flow from the patient and public to insurers and the government, and reimbursement dollars flow from insurers and the government to hospitals and doctors. Methods for reimbursing healthcare providers and facilities are frequently taught in courses addressing healthcare finance.  Unfortunately, defining the method of reimbursement and illustrating solutions to various problems incorporating these reimbursement methodologies often fails to convey the dynamic nature of payment systems or to set the context for informed decision-making.  System dynamics software provides an appropriate medium for demonstrating the flow of funds associated with healthcare reimbursement and for illustrating the impact of typical management decisions.  Three reimbursement methods are modeled generically: cost-based reimbursement, prospective payment, and capitation.

Cost-based reimbursement results in a payment to the provider based upon the cost of the resources consumed to provide care.  Until the advent of prospective payment systems in the United States in the early 1980s, hospitals were paid by Medicare and other payers on the basis of reasonable costs (Cleverley and Cameron, 2007; Gapenski, 2005).  Shi and Singh (2008) note that Medicare actually paid in excess of costs (“cost-plus”) because a percentage of capital costs were factored with operating costs into a formula used to compute a per diem reimbursement rate.  Neumann, et al. (1993) report that hospitals were paid reimbursable costs plus 2% from 1966 until 1970.  Cost-based reimbursement is a form of retrospective reimbursement – the amount to be paid to the provider is determined after the service is rendered.  The system dynamics model explicitly demonstrates why cost-based reimbursement (especially cost-plus) has fallen out of favor as a reimbursement method.

Prospective payment methods determine the amount to be paid to the provider before the service is rendered (Gapenski, 2005).  Diagnosis-Related Groups were introduced in 1983 as the method succeeding cost-based reimbursement to pay hospitals for Medicare inpatients in the United States.  Diagnoses coded from the International Classification of Diseases, 9^th Edition, Clinical Modification are currently assigned to 700+ MS-DRGs grouped by 25 major diagnostic categories (Cleverley and Cameron, 2007).  Other prospective payment methods have been subsequently adopted to include Ambulatory Payment Classification (APC) for outpatients and Resource Utilization Groups now in version 3 (RUG-III) for skilled nursing facilities (Castro and Layman, 2006).

Capitation represents a method to pay providers that is usually associated with managed care organizations in the United States.  The provider agrees to provide a menu of services to the managed care organization’s enrolled members in exchange for a prospective payment of x dollars per member per month [PMPM] (Cleverley and Cameron, 2007; Gapenski, 2005; Shi and Singh, 2008).

Explanation of Reimbursement Models

iThink® software was used to create the three generic healthcare reimbursement models:  Model 1 – Cost-Plus Reimbursement, Model 2 – Prospective Payment, and Model 3 – Capitation.  The models are a variation of cost-volume-profit analysis based upon the profit equation: Profit = Revenue – Costs.

Model 1 – Cost-Plus Reimbursement

Model 1, the Cost-Plus Reimbursement Model, is used to introduce system dynamics modeling.  Figure 1 provides the model’s schematic.

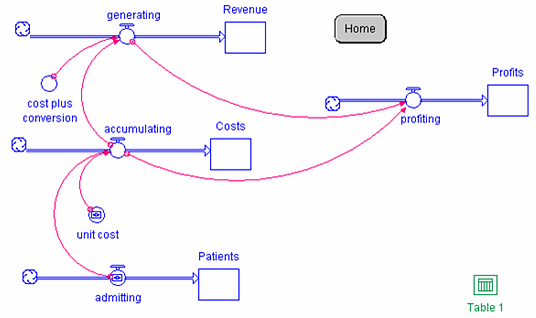
Figure 1.  Cost-Plus Reimbursement Model

In this model, patient admissions to the hospital drive reimbursement.  The flow admitting is initialized at 100 patients per month and patient admissions are recorded in the stock Patients.  The unit cost per admission is initialized at $500 as represented by the converter unit cost.  Costs accumulate at a rate of admitting times unit cost [100 patients per month x $500 per patient = $50,000 per month] as captured by the flow accumulating.  Patient costs are recorded in the stock Costs.  Revenue is generated by the recovery of costs plus 2% as represented by the converter cost plus conversion initialized at 1.02.  Therefore, revenue builds at a rate of accumulating x cost plus conversion [$50,000 per month x 1.02 = $51,000 per month] as captured by the flow generating.  Cumulative revenues are recorded in the stock Revenue.  Profits represent revenues minus costs, so the profit rate is represented by the flow profiting whose formula is generating minus accumulating [$51,000 - $50,000].  As initialized, the profit rate is $1,000 per month, so that annual profits are $12,000

Model 2 – Prospective Payment

Prospective payment methods establish payments in advance of treatment.  Figure 2 provides the schematic for Model 2, Prospective Payment.

Figure 2.  Prospective Payment Model

The stocks and flows representing patient admissions and the accumulation of costs are the same for Model 2 as Model 1.  Revenues are generated differently.  The revenue generated by each admission is established prospectively as captured by the converter unit revenue.   In order to produce the same initial profits, the prospective payment for each patient admitted is set by initializing the converter unit revenue to $510.  Therefore revenue builds at a rate of admitting x unit revenue [100 patients admitted per month x $510 per patient admitted = $51,000 per month] as captured by the flow generating.  Model 2 represents a simplification of real-world prospective payment models.  The prospective payment of $510 can either be thought of as one diagnosis (rather than many diagnoses represented by 700+ MS-DRGs) or thought of as the diagnostic case-mix represented by an average prospective payment.  Either way, the basic incentives associated with prospective payment remain the same.  Cumulative revenues are recorded in the stock Revenue.  Profits represent revenues minus costs, so the profit rate is once again represented by the flow profiting whose formula is generating minus accumulating [$51,000 - $50,000].  As the model is initialized, the profit rate is $1,000 per month, so that annual profits are $12,000.

Model 3 – Capitation

Modeling capitation rates is somewhat more complex.  Figure 3 provides the schematic for Model 3, Capitation.   Unlike cost-plus reimbursement and prospective payment, patient admissions to the hospital do not drive reimbursement, but they do determine costs.  Capitation involves up-front reimbursement of the provider at an established dollar per member per month ($PMPM) rate multiplied by the number of enrolled beneficiaries which are recorded by the converters $pmpm and covered lives, respectively.  The converter covered lives is initialized at 30,000 members, and the value for the converter $pmpm is set at $1.70 per member per month.  Therefore revenue builds at a rate of $pmpm x covered lives [$1.70 per member per month x 30,000 members = $51,000 per month] as captured by the flow generating.  Cumulative revenues are recorded in the stock Revenue.  Monthly admission rates under capitation depend upon covered lives, the annual service rate, and a monthly conversion factor as denoted by the converters covered lives, annual service rate, and monthly conversion, respectively.  Annual service rate is established at 40 admissions per 1000 members per year, and monthly conversion is established as 1 year per 12 months.  Therefore admissions build at a rate of covered lives x annual service rate x monthly conversion [30,000 members x 40 admissions per 1000 members per year x 1 year per 12 months = 100 admissions per month] as captured by the flow admitting.  The stocks and flows representing the accumulation of costs are the same for Model 3 as Models 1 and 2. 

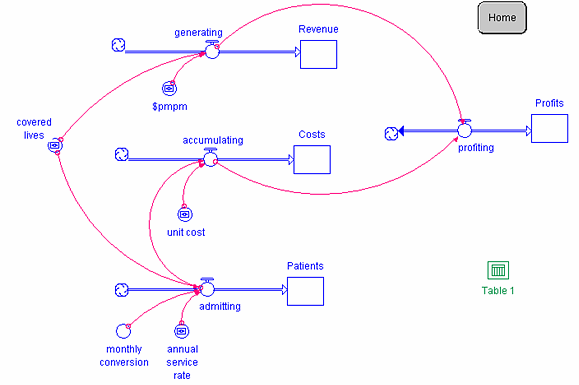
Figure 3.  Capitation Model

Profits represent revenues minus costs, so the profit rate is once again represented by the flow profiting whose formula is generating minus accumulating [$51,000 - $50,000].  As initialized, the profit rate is $1,000 per month, so that annual profits are $12,000.

Student/Model Interaction

The model interface is a “flight simulator” that allows the instructor or student to modify the value of selected model variables For Models 1 and 2, a slider can modify the converter unit cost within a range of $400 to $600 by increments of $10.  Similarly, a slider can be used to modify the converter admitting within a range of 75 to 125 admissions by increments of one.  A similar approach is taken for Model 3 except that a slider can be used to modify the values for the converter annual service rate within a range of 30 admissions per 1000 covered lives to 60 admissions per 1000 covered lives by increments of 10 which produces the same range of admissions from 75 to 125 as Models 1 and 2.  Model 3 is more complex than Models 1 and 2.  Covered lives and $PMPM are part of the negotiated contract and are beyond the immediate scope of decision-makers who may be able to influence unit costs and admissions.  Modifying these variables involves a second stage of decision-making, but sliders are included in the model interface to modify the converter covered lives within a range of 22,500 to 37,500 covered lives by increments of 100 lives and to modify the converter $pmpm within a range of $1.50 to $1.90 per member per month by increments of $0.10.

To begin model execution, the student is read a short narrative describing the reimbursement method incorporated into that model followed by a challenge to modify sliders one at a time to produce a configuration that maximizes profits.  The student interacts with the model in one of two ways.  The first form of interaction involves the instructor running each model as initialized and then seeking input about whether to increase or decrease the value of the sliders on subsequent runs.  The second form of interaction occurs with the student operating the software independently, but with the instructor standing by.  Each run result is posted to a comparative graph and a comparative table.

Table 1

 Run Results

Observation and Conclusions

Typical model runs have followed the pattern recorded by Table 1. 

The initial model explored is Model 1, Cost-Plus Reimbursement.  Run 1 proceeds at initialized values which produce an annual profit of $12,000.  Students are typically conditioned by the contemporary fiscal environment to reduce unit costs and run the model again.  Cutting unit costs to $400 for Run 2 produces a counterintuitive result; rather than increasing profits, a reduced profit of $9,600 is produced.  This result generally stimulates a class discussion which produces the insight that since unit revenue in this model is always 2% greater than unit costs, increasing, not reducing, costs is the optimal strategy.  Run 3 illustrates the result of simultaneously decreasing unit costs and admissions which produces the lowest profit of $7,200.  Run 4 illustrates the result of simultaneously increasing unit costs and admissions which produces the greatest profit of $18,000.

Figure 4 illustrates the model interface for Model 1 with sliders for unit cost and admitting and a comparative graph displaying the results of Runs 1 - 4.

Figure 4.  Model interface demonstrating typical runs for
Model 1, Cost-Plus Reimbursement Model.

Model 2, Prospective Payment, is usually explored next.  Again, Run 1 proceeds at initialized values which produce an annual profit of $12,000.  Students are conditioned by the contemporary fiscal environment to cut unit costs and run the model again.  Cutting unit costs to $400 for Run 2 produces an intuitive result; profits are increased to $132,000.  Follow-up discussion with the class usually reveals student understanding that since unit revenue is fixed, reductions in costs can produce dramatic increases in profit.  Holding unit cost constant at the lowest value of $400 and simultaneously decreasing admissions to 75 during Run 3 produces the expected result of a lower profit of $99,000.  Run 4 illustrates the optimal strategy of simultaneously decreasing unit costs and increasing admissions from the initialized values to $400 and 125 admissions which produces the greatest profit of $165,000.  Two additional runs typically produce additional insights.  If unit costs are set at $600 and admissions at 75 a loss of $81,000 is incurred.  Since the unit revenue of $510 is $90 less than the unit costs of $600, each additional admission produces additional losses, so that increasing admissions to 125 results in the loss of $135,000.

Model 3, Capitation, is usually explored next.  Again, Run 1 proceeds at initialized values which produce an annual profit of $12,000.  [Note - Setting annual service rate at 0.4 per covered life and covered lives at 30,000 produces a monthly admission rate of 100.]  Variables are manipulated in two stages, unit cost and annual service rate during stage one, and covered lives and $PMPM during stage two.  The variables not manipulated are held constant at initialized values.  The first stage perturbs variables whose values are likely to change during the operating year.  The second stage models variables reset upon review of the annual contract   Reducing unit costs to $400 for Run 2 produces the intuitive result; profits are increased to $132,000.  Follow-up discussion with the class usually reveals student understanding that since total revenue is fixed, reductions in costs can produce dramatic increases in profit.  Holding unit cost constant at the lowest value of $400 and simultaneously decreasing admissions by reducing the annual service rate to 0.03 during Run 3 increases profits to a maximum of $252,000.  Unlike Models 1 and 2, under capitation, total revenue is fixed by the capitated rate and number of enrolled beneficiaries.  Reducing service volume increases profits as demonstrated by Run 3; increasing service volume decreases profit as demonstrated by Run 4.  The greatest stage one loss of $288,000 is experienced during Run 5 when unit cost and annual service volume are both increased to their highest values.  Runs 6 – 13 illustrate the effects of holding unit cost and annual service rate constant while perturbing the values of covered lives and $PMPM in turn and then simultaneously.

Lessons learned by the students typically include:

• Different payment methods produce different incentives when pursuing even a simple goal like profit maximization.

• Cost-plus reimbursement is inherently inflationary.  If costs are always reimbursed plus a little more, the optimal strategy to maximize profits is to spend more.

• Prospective payment provides an incentive for the provider to reduce costs.  Reducing costs does not affect the payer, since the level of reimbursement has been determined ahead of time for the service provided.  If costs for providing a medical service are less than the prospectively determined reimbursement for that service, the profit maximizing strategy is to increase the volume of services.  This will cost the payer more.

• Capitation is more complex than either cost-plus reimbursement or prospective payment as indicated by the number of variables in the models.  Since total revenues are determined by covered lives times $PMPM, total revenues are usually fixed for the duration of the contracting period.  It is therefore very important that the negotiated $PMPM rate be negotiated at a level to produce sufficient revenue for the provider.  The provider has some ability to reduce unit costs and to reduce annual service rate during the contract period.  Since total revenue is fixed, reductions in either or both can dramatically improve profits.

• Anticipating the effects of simultaneous changes to two or more variables in a model is difficult.

Limitations

As presented, the system dynamics models are basic stock-flow representations of generic healthcare reimbursement systems.  Coupled with the “flight simulator” capabilities inherent in the software, students do gain insight into how manipulating variables within the decision-maker’s control affects profitability.  This is a useful and sufficient first lesson.  Additional complexity can be added by incorporating feedback loops and delays into the model in subsequent lessons.

References

Castro, A.B., & Layman, E.  (2006).  Principles of healthcare reimbursement.  American Health Information Management Association:  Chicago, IL.

Cleverley, W.O., & Cameron, A. E.  (2007).  Essentials of health care finance (6th ed.).  Jones and Bartlett Publishers: Sudbury, MA.

Gapenski, L. C.  (2005).  Healthcare finance: An introduction to accounting and financial management (3rd ed.).  Health Administration Press: Chicago, IL.

Getzen, T.  (2007).  Health economics and financing (3rd Ed.).  John Wiley & Sons, Inc.: Somerset, NJ.

Neumann, B. R., Suver, J.D., & Zelman, W. N.  (1993).  Financial management: Concepts and applications for health care providers (2nd ed.).  Kendall/Hunt Publishing Company:  Dubuque, IA

Shi, L., & Singh, D. A.  (2008).  Delivering health care in America: A systems approach (4th ed.).  Jones and Bartlett Publishers: Sudbury, MA.  

About the Author

Michael H. Kennedy PhD, MHA, FACHE is an Associate Professor in the Health Services and Information Management Department of the College of Allied Health Sciences at East Carolina University.  He has a PhD from Rensselaer Polytechnic Institute in Decision Sciences and Engineering Systems and a Masters in Health Administration from Baylor University. He has 33 years experience in teaching and health services administration that have been divided between both academic positions and operational assignments in the military health system as a human resources manager, equal opportunity advisor, ambulatory care administrator, and other positions of leadership culminating as the Chief Operating Officer of a small hospital.

In past academic assignments, Dr. Kennedy has served as Director of the Doctor of Health Administration Program at Central Michigan University, has taught in the Health Services Administration Program at Slippery Rock University, and was the Deputy Director of the U.S. Army-Baylor University Graduate Program in Healthcare Administration.

Dr. Kennedy is a Fellow in the American College of Healthcare Executives.

E-mail: kennedym@ecu.edu